Analytical Solutions
Confined Aquifer
Multi-well Variable-Rate Pumping-Test Analysis (click on the figure to enlarge)System Geometry
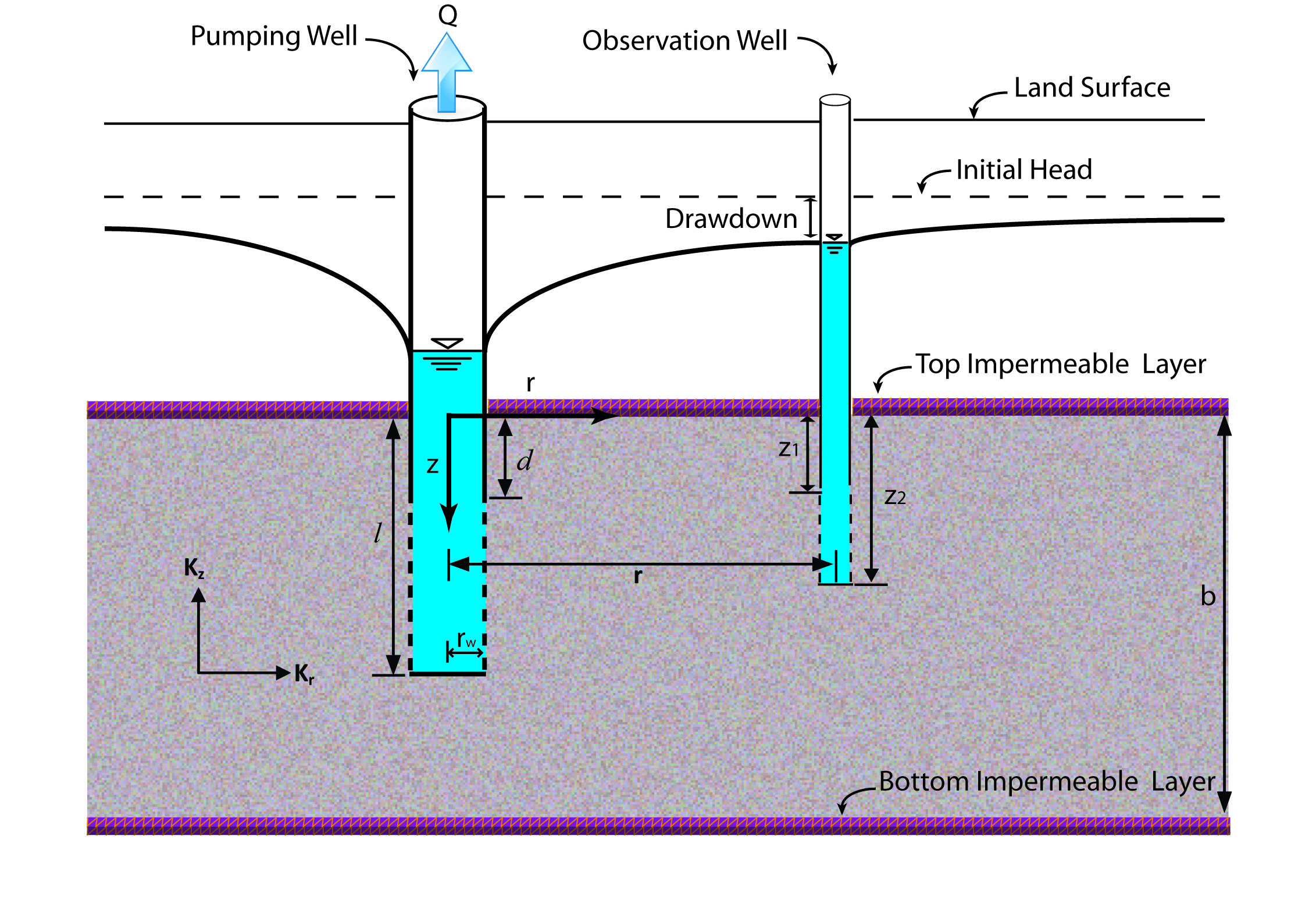
The schematic of system geometry for a confined aquifer (with an overlying and underlying aquitard) pumping test is shown in the adjacent figure.
The pumping well of finite radius rw is partially penetrating the confined aquifer of thickness b between depths l and d below the top impermeable boundary.
The pumping well has wellbore storage coefficient Cw (volume of water released from well storage per unit drawdown in it).
The observation well penetrating between depths z1 and z2 below the top impermeable boundary is located at distance r from the axis of the pumping well.
Analytical solutions for confined aquifers
The following analytical solutions are implemented in WELLS for confined aquifers:
- Theis [1935] Solution : For fully and partially penetrating well ( d=0, l=b ) of zero radius (rw = Cw =0 ) in an isotropic (Kr = Kz) confined aquifer.
- Hantush [1964] Solution : For partially penetrating well (0 ≤ d,l ≤ b ) of zero radius (rw = Cw =0 ) in an anisotropic (Kr ≠ Kz) confined aquifer.
- Papadopulos and Cooper [1967] Solution : For fully penetrating well (d=0, l=b ) of finite radius (rw ≠ 0 ) with a finite wellbore storage capacity (Cw ≠ 0 ) in an isotropic (Kr = Kz) confined aquifer solution :
- Yang et.al. [2006] Solution : For partially penetrating well (0 ≤ d,l ≤ b ) of finite radius (rw ≠ 0 ) with no wellbore storage capacity (Cw = 0 ) in an anisotropic (Kr ≠ Kz) confined aquifer.
- Mishra et.al. [2011] Solution : For partially penetrating well (0 ≤ d,l ≤ b ) of finite radius (rw ≠ 0 ) with a finite wellbore storage capacity (Cw ≠ 0 ) in an anisotropic (Kr ≠ Kz) confined aquifer.
References
- Theis, C.V., 1935. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage, Am. Geophys. Union Trans., vol. 16, pp. 519-524.
- Hantush, M.S., 1964. Hydraulics of wells, in: Advances in Hydroscience, V.T. Chow (editor), Academic Press, New York, pp. 281-442.
- Papadopulos, I.S. and H.H. Cooper, 1967. Drawdown in a well of large diameter, Water Resources Research, vol. 3, no. 1, pp. 241-244.
- S.‐Y. Yang, H.‐D. Yeh, and P. Chiu (2006), A closed form solution for constant flux pumping in a well under partial penetration condition, Water Resour. Res., 42, W05502, doi:10.1029/2004WR003889.
- Mishra P.K., V Vessilinov, S P Neuman, Radial flow towards large diamter well in a confined aquifer, Water Resources Research, In review.
Download
The WELLS code is available at no cost. Please follow the instructions on "Download" page.
Question/Comments
For questions/comments please fill out the information on the contact us page.